يشرح عالمان رياضيان كيف أن بناء الجسور داخل النظام ساعد في حل لغز عمره قرون

في 23 حزيران (يونيو) 1993 ، ألقى عالم الرياضيات أندرو وايلز آخر ثلاث محاضرات شرح فيها بالتفصيل حله لنظرية فيرما الأخيرة ، وهي مشكلة ظلت دون حل لمدة ثلاثة قرون ونصف. أحدث إعلان وايلز ضجة كبيرة ، سواء داخل المجتمع الرياضي أو في وسائل الإعلام.

بالإضافة إلى تقديم حل مرضٍ لمشكلة طويلة الأمد ، يمثل عمل ويلز لحظة مهمة في إنشاء جسر بين مجالين مهمين ، ولكن يبدو أنهما مختلفان تمامًا ، في الرياضيات.

يوضح التاريخ أن العديد من أعظم الاختراقات في الرياضيات تتضمن إقامة روابط بين فروع متباينة ظاهريًا للموضوع. تسمح هذه الجسور لعلماء الرياضيات ، مثلنا نحن الاثنين ، بنقل المشكلات من فرع إلى آخر والوصول إلى أدوات وتقنيات ورؤى جديدة.

ما هي نظرية فيرما الأخيرة؟

تشبه نظرية فيرما الأخيرة نظرية فيثاغورس ، التي تنص على أن أضلاع أي مثلث قائم الزاوية تعطي حلًا للمعادلة x² + ص² = ض² .

يعطي كل مثلث مختلف الأحجام حلاً مختلفًا ، وفي الواقع هناك عدد لا نهائي من الحلول حيث تكون كل من x و y و z أعدادًا صحيحة – أصغر مثال هو x = 3 و y = 4 و z = 5.

تدور نظرية فيرما الأخيرة حول ما يحدث إذا تغير الأس إلى شيء أكبر من 2. هل هناك حلول عدد صحيح لـ x³ + ص³ = ض³ ؟ ماذا لو كان الأس 10 أو 50 أو 30 مليون؟ أو بشكل عام ، ماذا عن أي رقم موجب أكبر من 2؟

في حوالي عام 1637 ، ادعى بيير دي فيرمات أن الإجابة كانت لا ، لا توجد ثلاثة أعداد صحيحة موجبة تمثل حلًا لـ x^ن + ص^ن = ض^ن لأي ن أكبر من 2. كتب عالم الرياضيات الفرنسي هذا الادعاء في هوامش نسخته من كتاب رياضيات من اليونان القديمة ، معلنا أن لديه دليلًا رائعًا على أن الهامش كان “ضيقًا جدًا بحيث لا يمكن احتواؤه”.

لم يتم العثور على دليل فيرما المزعوم ، واستمرت “نظريته الأخيرة” من الهوامش ، التي نشرها ابنه بعد وفاته ، في إصابة علماء الرياضيات بقرون عديدة.

البحث عن حل

على مدى 356 عامًا التالية ، لم يتمكن أحد من العثور على دليل فيرمات المفقود ، لكن لم يستطع أحد إثبات خطأه أيضًا – ولا حتى هومر سيمبسون. سرعان ما اكتسبت النظرية سمعة لكونها صعبة للغاية أو حتى من المستحيل إثباتها ، مع تقديم الآلاف من البراهين غير الصحيحة. حتى أن النظرية حصلت على مكان في موسوعة غينيس للأرقام القياسية باعتبارها “أصعب مشكلة في الرياضيات”.

هذا لا يعني أنه لم يكن هناك تقدم. لقد أثبت فيرمات نفسه من أجل n = 3 و n = 4. ساهم العديد من علماء الرياضيات الآخرين ، بما في ذلك الرائدة صوفي جيرمان ، في أدلة على القيم الفردية لـ n ، مستوحاة من طرق Fermat.

لكن معرفة أن نظرية فيرما الأخيرة صحيحة بالنسبة لأرقام معينة ليست كافية لعلماء الرياضيات – نحن بحاجة إلى معرفة أنها صحيحة بالنسبة للعديد منهم بلا حدود. أراد علماء الرياضيات إثباتًا يصلح لجميع الأعداد الأكبر من 2 في وقت واحد ، ولكن لقرون بدا الأمر وكأنه لا يمكن العثور على مثل هذا الدليل.

ومع ذلك ، في نهاية القرن العشرين ، اقترحت مجموعة متزايدة من الأعمال أن نظرية فيرما الأخيرة يجب أن تكون صحيحة. في قلب هذا العمل كان هناك شيء يسمى تخمين النمطية ، المعروف أيضًا باسم تخمين تانياما-شيمورا.

جسر بين عالمين

يقترح تخمين النمطية وجود علاقة بين كائنين رياضيين غير مرتبطين على ما يبدو: المنحنيات الإهليلجية والأشكال المعيارية.

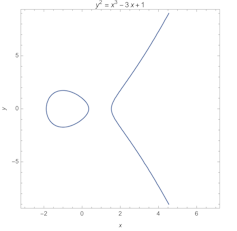
المنحنيات الإهليلجية ليست قطع ناقص ولا منحنيات. إنها مسافات على شكل دونات لحل المعادلات التكعيبية ، مثل y² = س³ – 3x + 1.

الشكل المعياري هو نوع من الوظائف التي تأخذ أعدادًا معقدة معينة – أرقامًا مكونة من جزأين: جزء حقيقي وجزء وهمي – وينتج عددًا مركبًا آخر. ما يجعل هذه الوظائف مميزة هو أنها متناظرة للغاية ، مما يعني أن هناك الكثير من الشروط على الشكل الذي يمكن أن تبدو عليه.

لا يوجد سبب لتوقع أن هذين المفهومين مرتبطان ، ولكن هذا ما يعنيه تخمين النمطية.

أخيرًا ، إثبات

لا يبدو أن حدسية النمطية تقول أي شيء عن المعادلات مثل x^ن + ص^ن = ض^ن . لكن عمل علماء الرياضيات في الثمانينيات أظهر وجود صلة بين هذه الأفكار الجديدة ونظرية فيرما القديمة.

أولاً ، في عام 1985 ، أدرك غيرهارد فراي أنه إذا كان فيرمات مخطئًا ويمكن أن يكون هناك حل لـ x^ن + ص^ن = ض^ن بالنسبة لبعض n أكبر من 2 ، ينتج عن هذا الحل منحنى إهليلجي غريب. ثم أوضح كينيث ريبيت في عام 1986 أن مثل هذا المنحنى لا يمكن أن يوجد في كون حيث كان تخمين النمطية صحيحًا أيضًا.

تضمن عملهم أنه إذا تمكن علماء الرياضيات من إثبات تخمين النمطية ، فيجب أن تكون نظرية فيرما الأخيرة صحيحة. بالنسبة للعديد من علماء الرياضيات ، بما في ذلك أندرو وايلز ، أصبح العمل على حدسية النمطية طريقًا لإثبات نظرية فيرما الأخيرة.

عمل وايلز لمدة سبع سنوات ، معظمها في الخفاء ، في محاولة لإثبات هذا التخمين الصعب. بحلول عام 1993 ، كان على وشك الحصول على دليل على حالة خاصة من التخمين المعياري – وهو كل ما يحتاجه لإثبات نظرية فيرما الأخيرة.

قدم عمله في سلسلة من المحاضرات في معهد إسحاق نيوتن في يونيو 1993. على الرغم من أن مراجعة الأقران اللاحقة وجدت فجوة في دليل وايلز ، عمل وايلز وطالبه السابق ريتشارد تيلور لمدة عام آخر لملء تلك الفجوة وتعزيز آخر فيرمات نظرية كحقيقة رياضية.

عواقب دائمة

تستمر تأثيرات نظرية فيرما الأخيرة وحلها في الارتداد عبر عالم الرياضيات. في عام 2001 ، قدمت مجموعة من الباحثين ، بما في ذلك تايلور ، دليلاً كاملاً على تخمين النمطية في سلسلة من الأوراق المستوحاة من عمل وايلز. كان هذا الجسر المكتمل بين المنحنيات البيضاوية والأشكال المعيارية – وسيظل – أساسًا لفهم الرياضيات ، حتى بعد نظرية فيرما الأخيرة.

يُستشهد بعمل وايلز على أنه بداية “حقبة جديدة في نظرية الأعداد” وهو أمر أساسي لأجزاء مهمة من الرياضيات الحديثة ، بما في ذلك تقنية تشفير مستخدمة على نطاق واسع وجهود بحثية ضخمة تُعرف باسم برنامج لانجلاندز الذي يهدف إلى بناء جسر بين عنصرين أساسيين مجالات الرياضيات: نظرية الأعداد الجبرية والتحليل التوافقي.

على الرغم من أن وايلز عمل في الغالب بمعزل عن الآخرين ، فقد احتاج في النهاية إلى مساعدة من أقرانه لتحديد وسد الفجوة في برهانه الأصلي. أصبحت الرياضيات اليوم على نحو متزايد مسعى تعاونيًا ، كما يتضح مما يتطلبه الأمر لإنهاء إثبات التخمين المعياري. المشاكل كبيرة ومعقدة وغالبًا ما تتطلب مجموعة متنوعة من الخبرات.

لذا ، أخيرًا ، هل كان لدى فيرمات حقًا دليل على نظريته الأخيرة ، كما ادعى؟ بمعرفة ما يعرفه علماء الرياضيات الآن ، لا يعتقد الكثير منا اليوم أنه فعل ذلك. على الرغم من أن فيرمات كان بارعًا ، إلا أنه كان مخطئًا في بعض الأحيان. يمكن لعلماء الرياضيات قبول أنه يعتقد أن لديه دليلًا ، لكن من غير المرجح أن يصمد دليله أمام التدقيق الحديث.